Representative-based Clustering ( K Means Clustering)
What is Clustering?
Clustering is the process of making a group of abstract objects into classes of similar objects.
Points to Remember
A cluster of data objects can be treated as one group.
While doing cluster analysis, we first partition the set of data into groups based on data similarity and then assign the labels to the groups.
The main advantage of clustering over classification is that, it is adaptable to changes and helps single out useful features that distinguish different groups.
Applications of Cluster Analysis
Clustering analysis is broadly used in many applications such as market research, pattern recognition, data analysis, and image processing.
Clustering can also help marketers discover distinct groups in their customer base. And they can characterize their customer groups based on the purchasing patterns.(customer segmentation)
In the field of biology, it can be used to derive plant and animal taxonomies, categorize genes with similar functionalities and gain insight into structures inherent to populations.
Clustering also helps in identification of areas of similar land use in an earth observation database. It also helps in the identification of groups of houses in a city according to house type, value, and geographic location.
Clustering also helps in classifying documents on the web for information discovery.
Clustering is also used in outlier detection applications such as detection of credit card fraud.
As a data mining function, cluster analysis serves as a tool to gain insight into the distribution of data to observe characteristics of each cluster.
Analyzing the trend on dynamic data
Example:
Scales to large data sets.
K-means would be faster than Hierarchical clustering if we had a high number of variables.
Guarantees convergence.
Easily adapts to new examples.
Generalizes to clusters of different shapes and sizes, such as elliptical clusters.
An instance’s cluster can be changed when centroids are re-computed.
When compared to Hierarchical clustering, K-means produces tighter clusters.
The order of the data has an impact on the final results.
Representative-based Clustering
Given a dataset with $n$ points in a d-dimensional space, $D = {x_i}_{i=1}^n$, and given the number of desired clusters $k$, the goal of representative-based clustering is to partition the dataset into $k$ groups or clusters, which is called a clustering and is denoted as $C =\{C_1,C_2,\ldots ,C_k\}$. Further, for each cluster $C_i$ there exists a representative point that summarizes the cluster, a common choice being the mean (also called the centroid) $\mu_i$ of all points in the cluster, that is,
$\mu_i=\frac{1}{n_i}\sum_{x_j \in C_i} x_j$
where $n_i=|C_i|$ is the number of points in cluster $C_i$.
A brute-force or exhaustive algorithm for finding a good clustering is simply to generate all possible partitions of $n$ points into $k$ clusters, evaluate some optimization score for each of them, and retain the clustering that yields the best score. The exact number of ways of partitioning $n$ points into $k$ nonempty and disjoint parts is given by the Stirling numbers of the second kind, given as
$S(n,k)=\frac{1}{k!}\sum_{t=0}^k (-1)^t\binom{k}{t}(k-t)^n$
Informally, each point can be assigned to any one of the $k$ clusters, so there are at most $k^n$ possible clusterings. However, any permutation of the $k$ clusters within a given clustering yields an equivalent clustering; therefore, there are $O(k^n/k!)$ clusterings of $n$ points into $k$ groups. It is clear that exhaustive enumeration and scoring of all possible clusterings is not practically feasible. In this we describe two approaches for representative-based clustering, namely the $K$-means and expectation-maximization algorithms.
K-MEANS ALGORITHM
Given a clustering $C =\{C_1,C_2,\ldots ,C_k\}$ we need some scoring function that evaluates its quality or goodness. This sum of squared errors scoring function is defined as
$SSE(C)=\sum_{i=1}^k\sum_{x_j \in C_i} || x_j-\mu_i||^2$
The goal is to find the clustering that minimizes the SSE score:
$C∗ = argmin_C \{SSE(C)\}$
K-means employs a greedy iterative approach to find a clustering that minimizes the SSE objective . As such it can converge to a local optima instead of a globally optimal clustering.
K-means initializes the cluster means by randomly generating k points in the data space. This is typically done by generating a value uniformly at random within the range for each dimension. Each iteration of K-means consists of two steps:
(1) cluster assignment, and
(2) centroid update.
Given the $k$ cluster means, in the cluster assignment step, each point $x_j \in D$ is assigned to the closest mean, which induces a clustering, with each cluster $Ci$ comprising points that are closer to $\mu_i$ than any other cluster mean.That is, each point $x_j$ is assigned to cluster $C_j^∗$ ,where
$j^∗ = argmin_{i=1}^k\{||xj −μi||^2\}$
Given a set of clusters $C_i , i = 1, \ldots ,k$, in the centroid update step, new mean values are computed for each cluster from the points in $C_i$ . The cluster assignment and centroid update steps are carried out iteratively until we reach a fixed point or local minima. Practically speaking, one can assume that K-means has converged if the centroids do not change from one iteration to the next. For instance, we can stop if $\sum_{ i=1}^k ||\mu_i^t-\mu_i^{t-1}||^2 \le \epsilon$,where $\epsilon > 0$ is the convergence threshold, $t$ denotes the current iteration, and $\mu_i^t$ denotes the mean for cluster $C_i$ in iteration $t $.
The pseudo-code for K-means is given in Algorithm below. Because the method starts with a random guess for the initial centroids, K-means is typically run several times, and the run with the lowest SSE value is chosen to report the final clustering. It is also worth noting that K-means generates convex-shaped clusters because the region in the data space corresponding to each cluster can be obtained as the intersection of half-spaces resulting from hyperplanes that bisect and are normal to the line segments that join pairs of cluster centroids.
In terms of the computational complexity of K-means, we can see that the cluster assignment step take $O(nkd)$ time because for each of the n points we have to compute its distance to each of the $k$ clusters, which takes $d$ operations in $d$ dimensions. The centroid re-computation step takes $O(nd)$ time because we have to add at total of $n$ $d$-dimensional points. Assuming that there are $t$ iterations, the total time for K-means is given as $O(tnkd)$. In terms of the I/O cost it requires $O(t)$ full database scans, because we have to read the entire database in each iteration.
The way kmeans algorithm works is as follows:
1.Specify number of clusters K.
2.Initialize centroids by first shuffling the dataset and then randomly selecting K data points for the centroids without replacement.
3.Keep iterating until there is no change to the centroids. i.e assignment of data points to clusters isn’t changing.
- Compute the sum of the squared distance between data points and all centroids.
- Assign each data point to the closest cluster (centroid).
- Compute the centroids for the clusters by taking the average of the all data points that belong to each cluster.
Example:Consider the one-dimensional data shown in Figure (a) below . Assume that we want to cluster the data into $k = 2$ groups. Let the initial centroids be $\mu_1 = 2$ and $\mu_2 = 4$. In the first iteration, we first compute the clusters, assigning each point to the closest mean, to obtain
$C_1 = \{2,3\}$ $C_2 = \{4,10,11,12,20,25,30\}$
We next update the means as follows:
$\mu_1 =\frac{2+3}{2}=2.5$
$\mu_2 =\frac{4+10+11+12+20+25+30}{7}=\frac{112}{7}=16$
The new centroids and clusters after the first iteration are shown in Figure(b).For the second step, we repeat the cluster assignment and centroid update steps, as shown in Figure(c), to obtain the new clusters:
$C_1 = \{2,3,4\}$ $C_2 = \{10,11,12,20,25,30\}$ and the new means:
$\mu_1 =\frac{2+3+4}{4}=\frac{9}{3}=3$
$\mu_2 =\frac{10+11+12+20+25+30}{6}=\frac{108}{6}=18$
The complete process until convergence is illustrated in Figure . The final clusters are given as
$C_1 = \{2,3,4,10,11,12\}$ $C_2 = \{20,25,30\}$
with representatives $\mu_1 = 7$ and $\mu_2 = 25$.
A1,B1,C1 are the initial centeroids
New centroids (2,10), (6,6),(1.5,3.5)
Advantage and Disadvantage of K-Means Clustering
Advantages
It is simple to grasp and put into practice.Scales to large data sets.
K-means would be faster than Hierarchical clustering if we had a high number of variables.
Guarantees convergence.
Easily adapts to new examples.
Generalizes to clusters of different shapes and sizes, such as elliptical clusters.
An instance’s cluster can be changed when centroids are re-computed.
When compared to Hierarchical clustering, K-means produces tighter clusters.
Disadvantages
It does not allow to develop the most optimal set of clusters and the number of clusters must be decided before the analysis. How many clusters to include is left at the discretion of the researcher. This involves a combination of common sense, domain knowledge, and statistical tools. Too many clusters tell you nothing because of the groups becoming very small and there are too many of them. There are statistical tools that measure within-group homogeneity and group heterogeneity. There are methods like the elbow method to decide the value of k. Additionally, there is a technique called a dendrogram. The results of a dendrogram analysis provide a recommendation of how many clusters to use. However, calculating a dendrogram for a large dataset could potentially crash a computer due to the computational load and the limits of RAM.
When doing the analysis, the k-means algorithm will randomly select several different places from which to develop clusters. This can be good or bad depending on where the algorithm chooses to begin at. From there, the centre of the clusters is recalculated until an adequate "centre'' is found for the number of clusters requested.
It’s quite sensitive to rescaling. If we rescale our data using normalization or standards, the outcome will be drastically different.
Centroids can be dragged by outliers, or outliers might get their own cluster instead of being ignored. Consider removing or clipping outliers before clustering.
Kmeans algorithm is good in capturing structure of the data if clusters have a spherical-like shape. It always try to construct a nice spherical shape around the centroid. That means, the minute the clusters have a complicated geometric shapes, kmeans does a poor job in clustering the data.
EXPECTATION-MAXIMIZATION CLUSTERING
The K-means approach is an example of a hard assignment clustering, where each point can belong to only one cluster. We now generalize the approach to consider soft assignment of points to clusters, so that each point has a probability of belonging to each cluster.
Let $D$ consist of $n$ points $x_j$ in $d$-dimensional space $R^d$ . Let $X_a$ denote the random variable corresponding to the $a$th attribute. We also use $X_a$ to denote the $a$th column vector, corresponding to the $n$ data samples from $X_a$. Let $X = (X_1,X_2,\ldots ,X_d )$ denote the vector random variable across the $d$-attributes, with $x_j$ being a data sample from X.
Gaussian Mixture Model
We assume that each cluster $C_i$ is characterized by a multivariate normal distribution, that is,
$f_i(x)=f(x|\mu_i,\Sigma_i)=\frac{1}{(2\pi)^{d/2}|\Sigma_i|^{1/2}}exp\{-\frac{(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)}{2}\}$
where the cluster mean $\mu_ \in R^d$ and covariance matrix $\Sigma_i \in R^{d×d}$ are both unknown parameters. $f_i (x)$ is the probability density at $x$ attributable to cluster $C_i$ . We assume that the probability density function of $X$ is given as a Gaussian mixture model over all the $k$ cluster normals, defined as
$f(x)=\sum_{i=1}^k f_i(x)P(C_i)=\sum_{i=1}^k f(x|\mu_i,\Sigma_i) P(C_i)$
where the prior probabilities $P(C_i)$ are called the mixture parameters, which must satisfy the condition
$\sum_{i=1}^k P(C_i)=1$
The Gaussian mixture model is thus characterized by the mean $\mu_i$ , the covariance matrix $\Sigma_i$ , and the mixture probability $P(C_i )$ for each of the $k$ normal distributions.We write the set of all the model parameters compactly as
$\theta = \{\mu_1,\Sigma_1,P(C_1 ) ,\ldots,\mu_k ,\Sigma_k,P(C_k )\}$
Maximum Likelihood Estimation
Given the dataset $D$, we define the likelihood of $\theta$ as the conditional probability of the data $D$ given the model parameters $\theta$, denoted as $P(D|\theta)$. Because each of the $n$ points $x_j$ is considered to be a random sample from $X$ (i.e., independent and identically distributed as $X$), the likelihood of $\theta$ is given as
The goal of maximum likelihood estimation (MLE) is to choose the parameters $\theta$ that maximize the likelihood, that is,
$\theta_∗ = argmax_θ \{P(D|θ)\}$
It is typical to maximize the log of the likelihood function because it turns the product over the points into a summation and the maximum value of the likelihood and log-likelihood coincide. That is, MLE maximizes
$\theta_∗ = argmax_θ \{ln P(D|θ)\}$
where the log-likelihood function is given as
$ln P(D|\theta)=\sum_{j=1}^n ln f(x_j)=\sum_{j=1}^n ln \left(\sum_{j=1}^k f(x_j|\mu_i,\Sigma_i) P(C_i)\right )$
Directly maximizing the log-likelihood over $\theta$ is hard. Instead, we can use the expectation-maximization (EM) approach for finding the maximum likelihood estimates for the parameters $\theta$. EM is a two-step iterative approach that starts from an initial guess for the parameters $\theta$. Given the current estimates for $\theta$, in the expectation step EM computes the cluster posterior probabilities $P(C_i |x_j )$ via the Bayes theorem:
Because each cluster is modeled as a multivariate normal distribution , the probability of $x_j$ given cluster $C_i$ can be obtained by considering a small interval $\epsilon > 0$ centered at $x_j$ , as follows:
The posterior probability of $C_i$ given $x_j$ is thus given as
$P(C_i|x_j)=\frac{f_i(x_j)P(C_i)}{\sum_{a=1}^k f_a(x_j).P(C_a)}$and $P(C_i |x_j )$ can be considered as the weight or contribution of the point $x_j$ to cluster $C_i$ . Next, in the maximization step, using the weights $P(C_i |x_j )$ EM re-estimates $\theta$,that is, it re-estimates the parameters $\mu_i , \Sigma_i $, and $P(C_i )$ for each cluster $C_i$ . The re-estimated mean is given as the weighted average of all the points, the re-estimated covariance matrix is given as the weighted covariance over all pairs of dimensions, and the re-estimated prior probability for each cluster is given as the fraction of weights that contribute to that cluster.
EM in One Dimension
Consider a dataset $D$ consisting of a single attribute $X$, where each point $x_j \in R (j = 1, . . . ,n)$ is a random sample from $X$. For the mixture model, we use univariate normals for each cluster:
$f_i(x)=f(x|\mu_i,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma_i}exp\{-\frac{(x-\mu_i)^2}{2\sigma_i^2}\}$
with the cluster parameters $\mu_i , \sigma_i^2$ , and $P(C_i )$. The EM approach consists of three steps:
initialization,
expectation step, and
maximization step.
Initialization
For each cluster $C_i$ , with $i = 1,2, . . . ,k$, we can randomly initialize the cluster parameters $\mu_i , \sigma_i^2$, and $P(C_i )$. The mean $\mu_i$ is selected uniformly at random from the range of possible values for $X$. It is typical to assume that the initial variance is given as $\sigma_i^2=1$. Finally, the cluster prior probabilities are initialized to $P(C_i ) = 1/k$ , so that each cluster has an equal probability.
Expectation Step
Assume that for each of the $k$ clusters, we have an estimate for the parameters, namely the mean $\mu_i $, variance $\sigma_i^2$,and prior probability $P(C_i )$. Given these values the clusters posterior probabilities are computed.
$P(C_i|x_j)=\frac{f(x_j|\mu_i,\sigma_i^2).P(C_i)}{\sum_{a=1}^k f(x_j|\mu_a,\sigma_a^2) P (C_a)}$
For convenience, we use the notation $w_{ij} =P(C_i |x_j )$, treating the posterior probability as the weight or contribution of the point $x_j$ to cluster $C_i$ . Further, let
$w_i = (w_{i1},\ldots ,w_{in})^T$
denote the weight vector for cluster $C_i$ across all the $n$ points.
Maximization Step
Assuming that all the posterior probability values or weights $w_{ij} = P(C_i |x_j )$ are known, the maximization step, as the name implies, computes the maximum likelihood estimates of the cluster parameters by re-estimating $\mu_i , \sigma_i^2$, and $P(C_i )$.
The re-estimated value for the cluster mean, $mu_i$ , is computed as the weighted mean of all the points:
In terms of the weight vector $w_i$ and the attribute vector $X = (x_1,x_2, \ldots ,x_n)^T$, we can
rewrite the above as
$\mu_i=\frac{w_i^T.X}{ w_i^T 1}$The re-estimated value of the cluster variance is computed as the weighted variance across all the points:
$\sigma_i^2=\frac{\sum_{j=1}^nw_{ij}(x_j-\mu_i)^2}{\sum_{j=1}^n w_{ij}}$
Let $Z_i = X − \mu_i 1 = (x_1 − \mu_i,x_2 − \mu_i , \ldots,x_n − \mu_i )^T = (z_{i1},z_{i2}, \ldots,z_{in})^T$ be the centered attribute vector for cluster $C_i$ , and let $Z_i^s$ be the squared vector given as
$Z_i^s= (z_{i1}^2, . . . ,z_{in}^2)^T$.
The variance can be expressed compactly in terms of the dot product between the weight vector and the squared centered vector:
$\sigma^2=\frac{w_i^TZ_i^s }{w_i^T 1}$
Finally, the prior probability of cluster $C_i$ is re-estimated as the fraction of the total weight belonging to $C_i $, computed as
$P(C_i)=\frac{\sum_{j=1}^n w_{ij}}{\sum_{a=1}^k \sum_{j=1}^n w_{aj}}=\frac{\sum_{j=1}^n w_{ij}}{\sum_{j=1}^n 1}=\frac{\sum_{j=1}^n w_{ij}}{n}$
where we made use of the fact that
$\sum_{i=1}{k} w_{ij} =\sum_{i=1}^k P(C_i|x_j)=1$
In vector notation the prior probability can be written as
$P(C_i)=\frac{w_i^T1}{n}$
Iteration
Starting from an initial set of values for the cluster parameters $\mu_i, \sigma_i^2$,and $P(C_i )$ for
all $i = 1, . . . ,k$, the EM algorithm applies the expectation step to compute the weights $w_{ij} = P(C_i |x_j )$. These values are then used in the maximization step to compute the updated cluster parameters $\mu_i , \sigma_i^2$ and $P(C_i )$. Both the expectation and maximization steps are iteratively applied until convergence, for example, until the means change very little from one iteration to the next.
Example:
EM in d Dimensions
We now consider the EM method in $d$ dimensions, where each cluster is characterized by a multivariate normal distribution , with parameters $\mu_i , \sigma_i$ , and $P(C_i )$.
For each cluster $C_i$ , we thus need to estimate the $d$-dimensional mean vector:
$\mu_i = (\mu_{i1},\mu_{i2},\ldots ,\mu_{id} )^T$
and the $d \times d$ in covariance matrix.If the dimensions are independent then we will end up with a diagonal covariance matrix
$\sum_i=\begin{bmatrix}(\sigma_1^i)^2 & 0 & \ldots & 0\\
0 & (\sigma_2^i)^2 & & \\
\vdots & \vdots & \ddots & \\
0& 0 & \ldots & (\sigma_d^i)^2
\end{bmatrix}$
Under the independence assumption we have only $d$ parameters to estimate for the diagonal covariance matrix.
Initialization
For each cluster $C_i$ , with i = 1,2, . . . ,k, we randomly initialize the mean $\mu_i$ by selecting a value $μ_{ia}$ for each dimension $X_a$ uniformly at random from the range of $X_a$ . The covariance matrix is initialized as the $d ×d$ identity matrix, $\Sigma_i = I$. Finally, the cluster prior probabilities are initialized to $P(C_i ) = 1/k$, so that each cluster has an equal probability.
Expectation Step
In the expectation step, we compute the posterior probability of cluster $C_i$ given point $x_j$ , with $i = 1, . . . ,k $Vand $j = 1, . . . ,n.$ As before, we use the shorthand notation $w_{ij} =P(C_i |x_j )$ to denote the fact that $P(C_i |x_j )$ can be considered as the weight or contribution of point $x_j$ to cluster $C_i$ , and we use the notation $w_i =(w_{i1},w_{i2},\ldots ,w_{in})^T$ to denote the weight vector for cluster $C_i$ , across all the $n$ points.
Maximization Step
Given the weights $w_{ij}$ , in the maximization step, we re-estimate $\sigma_i , \mu_i$ and $P(C_i )$. The mean $\mu_i$ for cluster $C_i$ can be estimated as
$\mu_i=\frac{\sum_{j=1}^n w_{ij} x_j}{\sum_{j=1}^n w_{ij}}$
which can be expressed compactly in matrix form as
$\mu_i=\frac{D^T.w_i}{ w_i^T 1}$
Let $Z_i = D−1 · \mu_i^T$ be the centered data matrix for cluster $C_i$ . Let $z_{ji} = x_j −\mu_i \in R^d$ denote the $j$ th centered point in $Z_i$ . We can express $\mu_i$ compactly using the outer-product form
Considering the pairwise attribute view, the covariance between dimensions $X_a$ and $X_b$ is estimated as
$\sigma_{ab}^i=\frac{\sum_{j=1}^n w_{ij}(x_{ja}-\mu_{ia})(x_{jb}-\mu_{ib}}{\sum_{j=1}^n w_{ij}}$
where $x_{ja}$ and $\mu_{ia}$ denote the values of the $a$th dimension for $x_j$ and $\mu_i$ , respectively.
Finally, the prior probability $P(C_i)$ for each cluster is the same as in the one-dimensional case
$P(C_i)=\frac{\sum_{j=1}^n w_{ij}}{n}=\frac{w_i^T 1}{n}$
EM Clustering Algorithm
The pseudo-code for the multivariate EM clustering algorithm is given below.After initialization of $\mu_i , \sigma_i$ , and $P(C_i )$ for all $i = 1, \ldots ,k$, the expectation and maximization steps are repeated until convergence. For the convergence test,we check whether $\sum_i=||\mu_i^t-\mu_i^{t-1}||^2 \le \epsilon$, where $\epsilon > 0$ is the convergence threshold, and $t$ denotes the iteration. In words, the iterative process continues until the change in the cluster means becomes very small.
Computational Complexity
For the expectation step, to compute the cluster posterior probabilities, we need to invert $\Sigma_i$ and compute its determinant $|\Sigma_i |$, which takes $O(d^3)$ time. Across the $k$ clusters the time is $O(kd^3)$. For the expectation step, evaluating the density $f (xj |\mu_i,\Sigma_i )$takes $O(d^2)$ time, for a total time of $O(knd^2)$ over the $n$ points and $k$ clusters. For the maximization step, the time is dominated by the update for $\Sigma_i$ , which takes $O(knd^2)$ time over all $k$ clusters. The computational complexity of the EM method is thus $O(t (kd^3 +nkd^2))$, where $t$ is the number of iterations. If we use a diagonal covariance matrix, then inverse and determinant of $\Sigma_i$ can be computed in $O(d)$ time. Density computation per point takes $O(d)$ time, so that the time for the expectation step is O(knd). The maximization step also takes $O(knd)$ time to re-estimate $\Sigma_i$ . The total time for a diagonal covariance matrix is therefore $O(tnkd)$. The I/O complexity for the EM algorithm is $O(t)$ complete database scans because we read the entire set of points in each iteration.
Python code for K-Means Clustering
# importing libraries
from sklearn.cluster import KMeans
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from matplotlib import pyplot as plt
#from sklearn.datasets import load_iris
%matplotlib inline
#reading and visualizing data
df=pd.read_csv("income.csv")
df.head()
plt.scatter(df['Age'],df['Incomes'])
#k means clustering with three clusters and setting a cluster prediction column
km=KMeans(n_clusters=3)
y_predict=km.fit_predict(df[['Age','Incomes']])
print(y_predict)
df['Cluster']=y_predict
df.head()
#creating 3 different data frames for 3 clusters and plotting in 3 different color
df1=df[df.Cluster==0]
df2=df[df.Cluster==1]
df3=df[df.Cluster==2]
plt.scatter(df1['Age'],df1['Incomes'],color='red')
plt.scatter(df2['Age'],df2['Incomes'],color='green')
plt.scatter(df3['Age'],df3['Incomes'],color='black')
Note that the clustering is not perfect this is because of the improper scale.We have to scale the data
x range is small y range is very high
# do the scaling
scaler=MinMaxScaler()
scaler.fit(df[['Incomes']])
df['Incomes']=scaler.transform(df[['Incomes']])
scaler.fit(df[['Age']])
df['Age']=scaler.transform(df[['Age']])
# redo the clustering
df.drop('Cluster',axis='columns',inplace=True)
km=KMeans(n_clusters=3)
y_predict=km.fit_predict(df[['Age','Incomes']])
print(y_predict)
df['Cluster']=y_predict
df.head()
df1=df[df.Cluster==0]
df2=df[df.Cluster==1]
df3=df[df.Cluster==2]
plt.scatter(df1['Age'],df1['Incomes'],color='red',label='red-C1')
plt.scatter(df2['Age'],df2['Incomes'],color='green',label='green-C2')
plt.scatter(df3['Age'],df3['Incomes'],color='black',label='black-C3')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],color='purple',marker='+',label='centroid')
plt.xlabel('Age')
plt.ylabel('Income')
plt.legend()
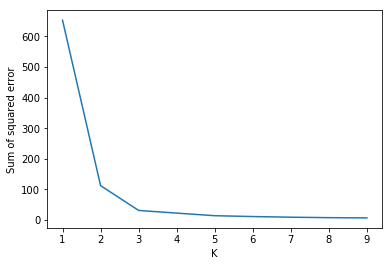
Elbow Method for optimal value of k in KMeans
We now define the following:-
Distortion: It is calculated as the average of the squared distances from the cluster centers of the respective clusters. Typically, the Euclidean distance metric is used.
Inertia: It is the sum of squared distances of samples to their closest cluster center.
To determine the optimal number of clusters, we have to select the value of $k$ at the “elbow” ie the point after which the distortion/inertia start decreasing in a linear fashion. Thus for the given data, we conclude that the optimal number of clusters for the data is 3.
sse = []
k_rng = range(1,10)
for k in k_rng:
km = KMeans(n_clusters=k)
km.fit(df)
sse.append(km.inertia_)
plt.xlabel('K')
plt.xlabel('K')
plt.ylabel('Sum of squared error')
plt.plot(k_rng,sse)
Simple Example with dummy data
#display the scatter plot of sample data
import matplotlib.pyplot as plt
x = [4, 5, 10, 4,
3, 11, 14 , 6, 10, 12]
y = [21, 19, 24, 17, 16, 25, 24, 22, 21, 21]
plt.scatter(x, y)
plt.show()
# finding the best value for k
from sklearn.cluster import KMeans
data = list(zip(x, y))
inertias = []
for i in range(1,11):
kmeans = KMeans(n_clusters=i)
kmeans.fit(data)
inertias.append(kmeans.inertia_)
plt.plot(range(1,11), inertias, marker='o')
plt.title('Elbow method')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.show()
#creating clusters and plotting
kmeans = KMeans(n_clusters=2)
kmeans.fit(data)
plt.scatter(x, y, c=kmeans.labels_)
plt.show()
kmeans.fit(data)
plt.scatter(x, y, c=kmeans.labels_)
plt.show()
Comments
Post a Comment